Cette formation est destinée :
• aux enseignants en mathématiques.
• formateurs en mathématiques.
• tuteurs d'enseignants en mathématiques.
• inspecteurs de mathématiques.
L'objectif est :
• d'attirer l'attention sur des traditions d'enseignement des mathématiques en France (ou leurs implicites) qui contribuent à la dégradation du niveau des mathématiques au secondaire, jusqu'à aboutir aux résultats catastrophiques des études TIMSS et PISA.
• de suggérer des présentations et des actions, palliant pour de nombreux élèves, à ces mauvais résultats.
Avec, ci-dessous, 12 des 25 rubriques présentes lors de la formation :
1. le piège des activités dites "préparatoires" ou "d'approche".
2. le piège (volontaire) des qcm faisant appel aux Systèmes 1 et 2 de D. Kahneman. Sans exercer les élèves à détecter ces pièges implicites.
3. le piège consistant à ne noter dans le cours que ce qui est vrai et rarement ce qui est faux.
4. l'absence généralement constatée de présentations simultanées du type : "dans ces cas oui" + "dans ces cas non".
5.en cours, l'absence d'assertions affirmées (avec nuances dans la signification et/ou l'ordre des mots) oralement par l'enseignant et sur lesquelles les élèves doivent voter par "vrai-faux" et argumenter (donc feedback immédiat à faire AVANT les exercices et non lors de la correction et l'installation de fausses croyances déjà faite).

6. dans le cahier de cours absence de mention EXPLICITE des combinaisons des propriétés d'abord présentées séparément. La rencontre avec ces combinaisons étant généralement reportées aux exercices à faire et ainsi, ne permettent pas à certains élèves de savoir si ces combinaisons sont TOUJOURS POSSIBLES, ou seulement dans tel ou tel exercice ...
7. le piège consistant à "zapper" les raisonnements naturels de la "vraie vie", avant de les codifier par les notations et le vocabulaire mathématiques.
8. la rare présence des analogies de la "vraie vie", qui pourtant apportent du sens et des débuts de mémorisation pour de nombreux éléves.
Exemple : dans l'étude TIMMS, l'ample échec face à la notion de ratio (par exemple ratio 3:2). Alors qu'en prenant l'analogie du résultat d'un match de football "Marseille-Lyon" traditionnellement présenté sous la forme "Marseille 3 : Lyon 2" (que quasime,nt tout le monde connait, et en demandant combien de buts Marseille a marqué, parmi le total de buts du match qui est égal à 5, on arrive facilement à traduire la notation "ratio" 3:2 par par la fraction 3/5 (pour Marseille).
9. la séparation dans le temps de deux leçons qui sont pourtant liées par un raisonnement "identique" mais inverse (comme la classique séparation de la leçon sur l'exponentielle et celle du logarithme).
10. la rare présence dans le cahier de cours, de la présentation d'une même notion sous 3 formes différentes : graphique, classiquement littérale, cause-conséquences.
11. dans le cahier de cours, absence de récapitulatif des différentes méthodes vues lors des années antérieures, toujours valables ET dont l'utilisation est souvent bienvenue dans des exercices des classes suivantes ... MAIS les élèves n'y pensent plus.
12. absence de demande de reformulation du cours en guise de travail à la maison (sur Fiche de Cornell par exemple).
Et bien entendu, les parades déjà prêtes pour contourner ces pièges-freins- facteurs d'égarement.
Elargir la palette méthodologique dont on dispose est souvent déterminant pour "débloquer" certains élèves-étudiants.
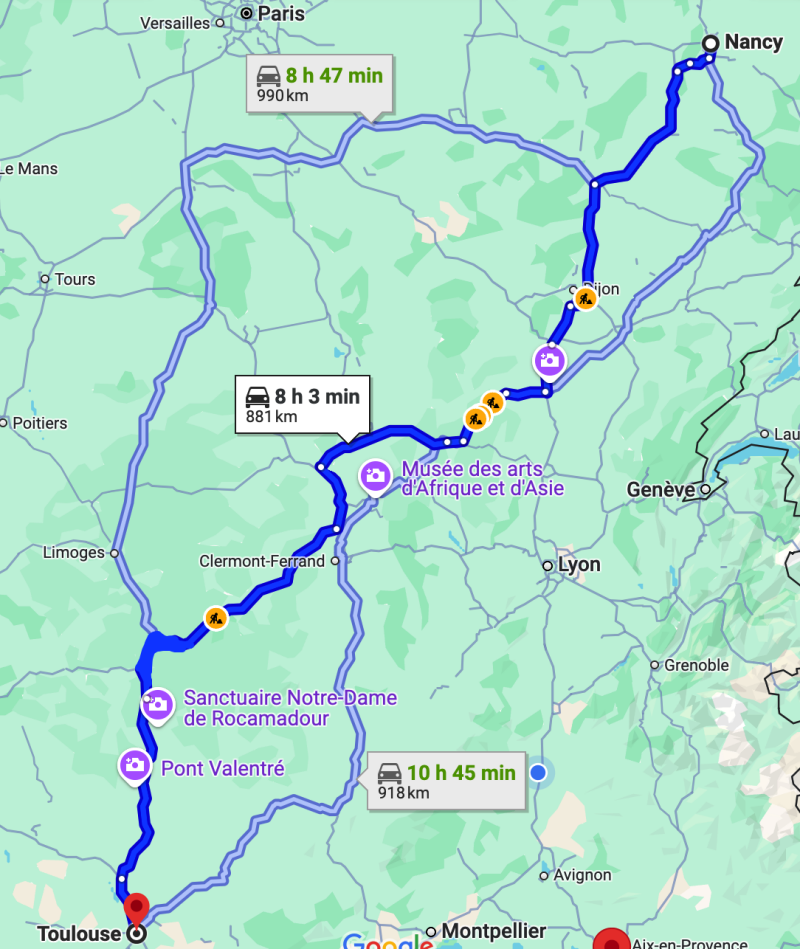
Analogie avec les trajets routiers proposés par un GPS :
Etape 1 :
Constater que, pour aller de Nancy à Toulouse, il y a plusieurs chemins routiers possibles (en voici quelques-uns) :
Etape 1 de l'idée mathématique :
Exemple : rappeler à des élèves de Terminale qu'il y a plusieurs stratégies possibles pour parvenir à montrer que deux droites de l'espace sont orthogonales :
• somme des angles dans un triangle.
• réciproque de Pythagore.
• multiplication des coefficients directeurs.
• produit scalaire (4 formules possibles).
• colinéarité des vecteurs normaux et des vecteurs directeurs.
• vecteur normal à un plan.
• relation d'Al-Kashi.
Etc.
Etape 2 :
En supposant que les symboles "travaux" signifient que la route est carrément coupée à ces endroits, on en déduit évidemment que ce trajet est à écarter de ceux que l'on va pouvoir emprunter.

Etape 2 de l'idée mathématique :
Dans la foulée, proposer des situations où certaines de ces stratégies ne pourront pas être utilisées (en maths : souvent faute d'informations disponibles pour le pouvoir).
Exemple : dans l'énoncé, on ne dispose d'aucun angle.
Etape 3 :
On suppose que les trois chemins proposés sont : le trajet le plus court, le trajet le plus rapide, le trajet évitant les péages. En déduire celui que l'on souhaite emprunter.
Etape 3 de l'idée mathématique:
Finir par proposer des situations, où quelques-unes des stratégies possibles sont "disponibles", MAIS où l'énoncé ajoute une exigence à satisfaire.
Exemple : l'énoncé demande de montrer que le point H est le projeté orthogonal de A, sur la droit (CD).